Unveiling the intricacies of geometry, Big Ideas Math Geometry 12.2 Answers provides a comprehensive guide to angle relationships and polygon properties, empowering students to unravel the secrets of shapes and their interactions.

Delving into the depths of complementary, supplementary, and vertical angles, this chapter equips learners with the tools to decipher the unknown measures of angles. Angle bisectors and perpendicular bisectors emerge as crucial concepts, revealing their role in constructing and analyzing geometric figures.

Big Ideas Math Geometry 12.2 Overview

Big Ideas Math Geometry Chapter 12.2 delves into the fascinating realm of circles, introducing students to their defining characteristics and exploring their properties and applications.

The chapter aims to equip students with a comprehensive understanding of circles, enabling them to analyze and solve problems involving these fundamental geometric shapes.

Key Concepts

• Definition of a circle and its key elements: center, radius, diameter, and chord
• Properties of chords, tangents, and secants
• Angle measures and relationships within circles, including inscribed angles and central angles
• Arc measures and their relationship to central angles
• Applications of circles in real-world contexts, such as architecture, engineering, and design

Learning Objectives

• Define a circle and identify its essential components.
• Apply the properties of chords, tangents, and secants to solve problems.
• Calculate angle measures and relationships within circles using inscribed angles and central angles.
• Determine arc measures and their relationship to central angles.
• Utilize circles in practical applications across various disciplines.

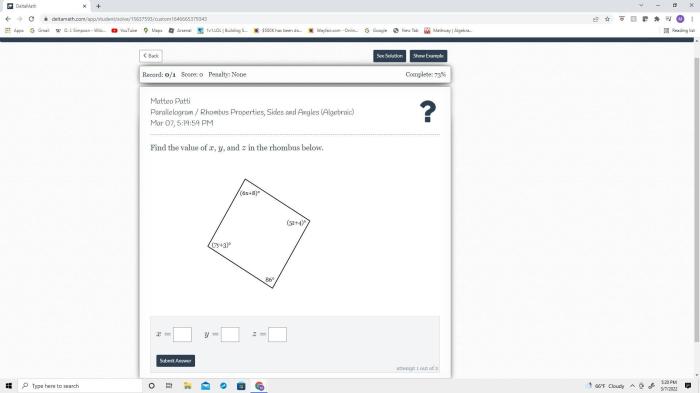
Angle Relationships

Angle relationships describe the ways in which angles interact with each other. Understanding these relationships is crucial for solving geometry problems and understanding the properties of shapes.

There are several types of angle relationships, including:

Complementary Angles

• Complementary angles are two angles whose measures add up to 90 degrees.
• Complementary angles are often found in pairs, such as the angles formed by two perpendicular lines.
• To find the measure of an unknown complementary angle, subtract the measure of the known angle from 90 degrees.

Supplementary Angles

• Supplementary angles are two angles whose measures add up to 180 degrees.
• Supplementary angles are often found in pairs, such as the angles formed by two adjacent lines.
• To find the measure of an unknown supplementary angle, subtract the measure of the known angle from 180 degrees.

Vertical Angles, Big ideas math geometry 12.2 answers

• Vertical angles are two angles that are formed by two intersecting lines.
• Vertical angles are always congruent, meaning they have the same measure.
• To find the measure of an unknown vertical angle, simply find the measure of one of the angles.

Angle relationships are essential for understanding the properties of shapes and solving geometry problems. By understanding these relationships, students can develop a deeper understanding of geometry and its applications.

Angle Bisectors and Perpendicular Bisectors

Angle bisectors and perpendicular bisectors are two important constructions in geometry. An angle bisector is a line that divides an angle into two equal parts, while a perpendicular bisector is a line that passes through the midpoint of a line segment and is perpendicular to it.

Angle Bisectors

An angle bisector can be constructed using a compass and straightedge. To construct an angle bisector, follow these steps:

• Draw an arc that intersects both sides of the angle.
• Draw a second arc with the same radius that intersects the first arc.
• Connect the points of intersection of the two arcs with a line.

The line drawn in step 3 is the angle bisector.

Perpendicular Bisectors

A perpendicular bisector can also be constructed using a compass and straightedge. To construct a perpendicular bisector, follow these steps:

• Draw a circle with the same radius as the line segment.
• Place the center of the circle at the midpoint of the line segment.
• Draw two lines tangent to the circle that pass through the endpoints of the line segment.

The line that connects the points of tangency is the perpendicular bisector.

Properties of Angle Bisectors and Perpendicular Bisectors

Angle bisectors and perpendicular bisectors have a number of important properties. Some of these properties include:* An angle bisector divides an angle into two congruent angles.

• A perpendicular bisector bisects a line segment into two congruent segments.
• The perpendicular bisector of a line segment is perpendicular to the line segment at its midpoint.
• The angle bisector of an angle is the perpendicular bisector of the opposite side of the angle.

These properties make angle bisectors and perpendicular bisectors useful for a variety of geometric constructions.

Midsegments and Medians

Midsegments and medians are two types of line segments that can be drawn in a triangle. They have different definitions, constructions, and properties.

Midsegments

A midsegment of a triangle is a line segment that connects the midpoints of two sides of the triangle. To construct a midsegment, find the midpoint of each side of the triangle, then connect the midpoints with a line segment.

The midsegment is parallel to the third side of the triangle and half its length.Midsegments have the following properties:

• They are parallel to the third side of the triangle.
• They are half the length of the third side of the triangle.
• They divide the triangle into two congruent triangles.

Medians

A median of a triangle is a line segment that connects a vertex of the triangle to the midpoint of the opposite side. To construct a median, find the midpoint of one side of the triangle, then connect the midpoint to the opposite vertex.

The median divides the triangle into two equal areas.Medians have the following properties:

• They connect a vertex to the midpoint of the opposite side.
• They divide the triangle into two equal areas.
• They intersect at a point called the centroid of the triangle.

Midsegments and medians are both important line segments in a triangle. They can be used to find the midpoint of a side, to divide the triangle into equal areas, and to find the centroid of the triangle.

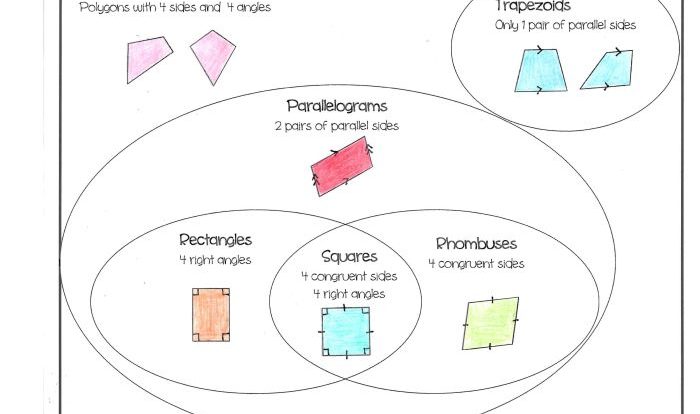
Polygons: Big Ideas Math Geometry 12.2 Answers

In geometry, a polygon is a plane figure that is bounded by a finite number of straight line segments that are joined to form a closed shape. The line segments are called sides, and the points where they meet are called vertices.

A polygon with three sides is called a triangle, a polygon with four sides is called a quadrilateral, a polygon with five sides is called a pentagon, and so on.

Polygons can be classified into two main types: regular and irregular. A regular polygon is a polygon in which all sides are equal in length and all angles are equal in measure. An irregular polygon is a polygon in which the sides and/or angles are not all equal.

Properties of Regular Polygons

Regular polygons have a number of interesting properties. Some of these properties include:

• All sides are congruent.
• All angles are congruent.
• The sum of the interior angles of a regular polygon with n sides is (n-2)180 degrees.
• The area of a regular polygon with n sides, each of length s, is given by the formula A = (1/4)ns^2 cot(180/n) degrees.

Types of Polygons

There are many different types of polygons. Some of the most common types include:

• Triangle: A polygon with three sides.
• Quadrilateral: A polygon with four sides.
• Pentagon: A polygon with five sides.
• Hexagon: A polygon with six sides.
• Octagon: A polygon with eight sides.
• Decagon: A polygon with ten sides.

Similar Polygons

Similar polygons are polygons that have the same shape but not necessarily the same size. The corresponding angles of similar polygons are congruent, and the corresponding sides are proportional.

Conditions for Similarity of Polygons

There are three conditions for similarity of polygons:

1. The corresponding angles of the polygons are congruent.
2. The corresponding sides of the polygons are proportional.
3. The polygons have the same number of sides.

Properties of Similar Polygons

Similar polygons have the following properties:

• The ratios of the corresponding sides are equal.
• The ratios of the corresponding diagonals are equal.
• The ratios of the corresponding areas are equal to the square of the ratio of the corresponding sides.
• The ratios of the corresponding perimeters are equal to the ratio of the corresponding sides.

Question Bank

What are the key concepts covered in Big Ideas Math Geometry 12.2?

Angle relationships, angle bisectors, perpendicular bisectors, midsegments, medians, and polygons.

How can I find the measure of an unknown angle using angle relationships?

Use the properties of complementary, supplementary, and vertical angles to establish relationships between known and unknown angles.

What is the difference between an angle bisector and a perpendicular bisector?

An angle bisector divides an angle into two equal parts, while a perpendicular bisector divides a line segment into two equal parts and is perpendicular to the line segment.